Закон Харди - Вайнберга
Генофонд популяции может быть описан либо частотами генов, либо частотами генотипов. Представим себе, что в популяция имеется N диплоидных особей, различающихся по одной паре аллелей (А и a); D - означает число гомозигот по доминантному аллелю (АА); Р - число гомозигот по рецессивному аллелю (аа); Н - число гетерозигот (Аа). Таким образом, в популяции будет существовать три типа особей, имеющих соответственно генотипы АА, Аа, аа. Поскольку каждая особь с генотипом АА имеет два аллеля А, а каждый индивидуум Аа - по одному аллелю А, общее число аллелей А составит 2D+Н. Тогда р - частота встречаемостидоминантного аллеля А равна:
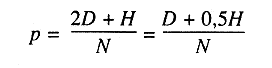
Частоту рецессивного аллеля (а) принято обозначать q. Сумма частот генов А и а равняется единице, р+q=1, отсюда q=1-р. Если ген представлен только двумя аллелями (А и а) с частотой р и q, то каковы будут частоты трех возможных генотипов?
На поставленный вопрос дает ответ закон Харди - Вайнберга. На первый взгляд может показаться, что особи с доминантным фенотипом будут встречаться чаще, чем с рецессивным. Однако отношение 3:1 соблюдается лишь в потомстве двух гетерозиготных по одним и тем же аллелям особей. Законы Менделя ничего не говорят о частотах генотипов и фенотипов в популяциях. О них идет речь в названном законе. Его сформулировали независимо друг от друга математик Дж. Харди в Англии и врач Вильгельм Вайнберг в Германии. Чтобы понять смысл этого закона, предположим, что самцы и самки в популяции скрещиваются случайно, или, что одно и то же, гаметы самцов и самок будут комбинироваться случайно, образуя зиготы. В зиготе объединяются материнские и отцовские хромосомы, каждая из гомологичных хромосом несет по одному аллелю из данной пары. Образование особей с генотипом АА обусловлено вероятностью получения аллеля А от матери и аллеля А от отца, т.е. рхр = р2.
Аналогично возникновение генотипа аа, частота встречаемости которого равна q2. Генотип Аа может возникнуть двумя путями: организм получает аллель А от матери, аллель а - от отца или, наоборот, аллель А - от отца, аллель а - от матери. Вероятность того и другого события равна pq, а суммарная вероятность возникновения генотипа Аа равна 2pq. Таким образом, частоту трех возможных генотипов можно выразить уравнением: (p+q)2=p2+2pq+q2=1
Из уравнения следует, что если скрещивание случайно, то частоты генотипов связаны с частотами аллелей простыми соотношениями по формуле бинома Ньютона.
Разберем пример, когда частоты аллей данного гена в популяции будут 0,1А; 0,3a (геометрическое выражение закона Харди - Вайнберга для этого случая представлено на рис. 21 ). В потомстве на 100 зигот будет 49 гомозигот АА, 9 гомозигот аа и 42 гетерозиготы Аа, т.е. это соответствует уже известному нам соотношению генотипов - р2(АА) : 2pq(Ad): q2(aa).
Интересно, что в следующем поколении гаметы с аллелем А будут возникать с частотой 0,7 (0,49 от гомозигот АА +0,21 от гетерозигот Aa). Данное соотношение сохранится и в будущем. Частоты генов, а соответственно и генотипов остаются неизменными из поколения в поколение - это одно из основных положений закона Харди - Вайнберга. Однако названный закон носит вероятностный характер и поэтому реализуется в бесконечно большой популяции. При этом частоты генов остаются неизменными, если: существует неограниченная панмиксия; отсутствует естественный отбор; не возникают новые мутации тех же генов; не происходит миграция особей с иными генотипами из соседних популяций.
Однако эти процессы постоянно происходят в природе и обусловливают микроэволюцию, сущность которой противоречит основному положению закона Харди - Вайнберга и в генетическом смысле сводится к изменению частот аллелей в популяции. С помощью закона Харди - Вайнберга, зная частоту встречаемого гомозиготных носителей рецессивного признака (q2) в популяции, можно рассчитать частоту гетерозигот (2рq) и частоту гомогозигот но доминантному аллелю (р2).
См. Равновесие Харди-Вайнберга